5.3 - Prueba de la primera derivada para la determinación de máximos y mínimos:

  

5.2 - Extremos relativos y extremos absolutos:

Si f es derivable en a, a es un extremo relativo o local si:

Si f'(a) = 0.

Si f''(a) ≠ 0.

Máximos relativos

Si f y f' son derivables en a, a es un máximo relativo si se cumple:

f'(a) = 0

f''(a) < 0

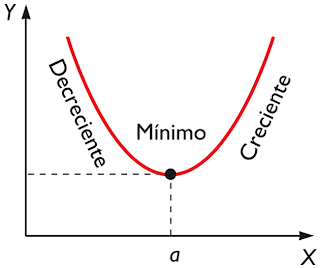
Mínimos relativos

Si f y f' son derivables en a, a es un mínimo relativo si se cumple:

f'(a) = 0

f''(a) > 0

5.1 - Función creciente y decreciente:

Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x₁  y x₂, con la condición x₁ £ x₂, se verifica que

 f( x₁ ) < f( x₂ ).

Se dice estrictamente creciente si de x₁ < x₂ se deduce que f(x₁) < f(x₂).

 Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x₁  y x₂, que cumplan x₁ £ x₂, entonces f(x₁ ) ³ f(x₂ ).

Siempre que de x₁ < x₂ se deduzca f(x₁ ) > f(x₂ ), la función se dice estrictamente decreciente.

Una función es creciente en un punto a si existe un intervalo abierto

f(x) £ f(a) si x pertenece a (a - e, a) y

f(x) ³ f(a) si x pertenece a (a, a + e).

https://www.youtube.com/watch?v=rKjPXCGgyOQ

4.6 - Diferenciales:

En matemáticas, concretamente en cálculo diferencial, el diferencial es un objeto matemático que representa la parte principal del cambio en la linealización de una funcióny = ƒ(x) con respecto a cambios en la variable independiente.

Sea f(x) una función derivable. Diferencial de una función correspondiente al incremento h de la variable independiente, es el producto f'(x) · h. Se representa por dy.

4.5 - Derivadas de orden superior:

La derivada de la derivada de una función se conoce como segunda derivada de la función, es decir, si f(x) es una función y existe su primera derivada f´(x), en el caso de que se pueda obtener, la derivada de la función obtenida de aplicar la derivada se le llama segunda derivada:

de manera similar se puede obtener las derivadas de mayor orden, sin embargo es necesario aclarar que las derivadas de una función dependen de las características de la función y es posible, y frecuentemente sucede, que algunas derivadas existen pero no para todos los ordenes pese a que se puedan calcular con las formulas.

 4.4 - Diferenciación logarítmica:

Con determinadas funciones, especialmente para la función potencial-exponencial, es aconsejable el empleo de la derivación logarítmica, ya que facilitan bastante el cálculo.

4.3 - Diferenciación implícita:

Se dice que una función está definida explícitamente cuando se da de la forma y = f (x); esto es cuando se da y despejada en términos de x. En cambio, si en una ecuación, como por ejemplo, 2yx = cos3y, existe una función tal que y = f (x), se dice que y es una función que está definida implícitamente por la ecuación. Una ecuación en x e y puede definir a más de una función implícita.
v    En muchas ocasiones no se puede resolver explícitamente una función dada en forma implícita.
v    Es posible hallar la derivada de una función expresada implícitamente, sin necesidad de transformarla en su equivalente explícita.

aquí podrán ver un ejemplo de como hacerlo

https://www.youtube.com/watch?v=oneC1gsSQaM

4.2 - Derivadas de funciones exponenciales:

La derivada de la función exponencial ea igual a la misma función por el logaritmo neperiano de la base y por la derivada del exponente.

La derivada de la función exponencial de base e ea igual a la misma función por la derivada del exponente.

4.1 - Derivadas de funciones logarítmicas:

En el ámbito de las matemáticas, específicamente en el cálculo y el análisis complejo, la derivada logarítmica de una función f queda definida por la fórmula

donde f ′ es la derivada de f.

Cuando f es una función f(x) de una variable real x, y toma valores reales, estrictamente positivos, esta es entonces la fórmula para (log f)′, o sea, la derivada del logaritmo natural de f, como se deduce aplicando directamente la regla de la cadena.