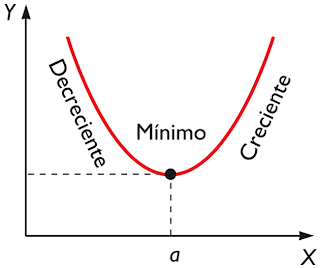
5.1 - Función creciente y decreciente:

Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x₁  y x₂, con la condición x₁ £ x₂, se verifica que

 f( x₁ ) < f( x₂ ).

Se dice estrictamente creciente si de x₁ < x₂ se deduce que f(x₁) < f(x₂).

 Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x₁  y x₂, que cumplan x₁ £ x₂, entonces f(x₁ ) ³ f(x₂ ).

Siempre que de x₁ < x₂ se deduzca f(x₁ ) > f(x₂ ), la función se dice estrictamente decreciente.

Una función es creciente en un punto a si existe un intervalo abierto

f(x) £ f(a) si x pertenece a (a - e, a) y

f(x) ³ f(a) si x pertenece a (a, a + e).

https://www.youtube.com/watch?v=rKjPXCGgyOQ