5.3 - Prueba de la primera derivada para la determinación de máximos y mínimos:

  

5.2 - Extremos relativos y extremos absolutos:

Si f es derivable en a, a es un extremo relativo o local si:

Si f'(a) = 0.

Si f''(a) ≠ 0.

Máximos relativos

Si f y f' son derivables en a, a es un máximo relativo si se cumple:

f'(a) = 0

f''(a) < 0

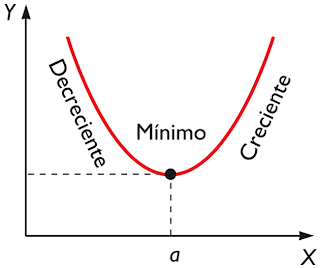
Mínimos relativos

Si f y f' son derivables en a, a es un mínimo relativo si se cumple:

f'(a) = 0

f''(a) > 0

5.1 - Función creciente y decreciente:

Una función es creciente en un intervalo [a,b] si al tomar dos puntos cualesquiera del mismo, x₁  y x₂, con la condición x₁ £ x₂, se verifica que

 f( x₁ ) < f( x₂ ).

Se dice estrictamente creciente si de x₁ < x₂ se deduce que f(x₁) < f(x₂).

 Una función es decreciente en un intervalo [a,b] si para cualesquiera puntos del intervalo, x₁  y x₂, que cumplan x₁ £ x₂, entonces f(x₁ ) ³ f(x₂ ).

Siempre que de x₁ < x₂ se deduzca f(x₁ ) > f(x₂ ), la función se dice estrictamente decreciente.

Una función es creciente en un punto a si existe un intervalo abierto

f(x) £ f(a) si x pertenece a (a - e, a) y

f(x) ³ f(a) si x pertenece a (a, a + e).

https://www.youtube.com/watch?v=rKjPXCGgyOQ

4.6 - Diferenciales:

En matemáticas, concretamente en cálculo diferencial, el diferencial es un objeto matemático que representa la parte principal del cambio en la linealización de una funcióny = ƒ(x) con respecto a cambios en la variable independiente.

Sea f(x) una función derivable. Diferencial de una función correspondiente al incremento h de la variable independiente, es el producto f'(x) · h. Se representa por dy.

4.5 - Derivadas de orden superior:

La derivada de la derivada de una función se conoce como segunda derivada de la función, es decir, si f(x) es una función y existe su primera derivada f´(x), en el caso de que se pueda obtener, la derivada de la función obtenida de aplicar la derivada se le llama segunda derivada:

de manera similar se puede obtener las derivadas de mayor orden, sin embargo es necesario aclarar que las derivadas de una función dependen de las características de la función y es posible, y frecuentemente sucede, que algunas derivadas existen pero no para todos los ordenes pese a que se puedan calcular con las formulas.

 4.4 - Diferenciación logarítmica:

Con determinadas funciones, especialmente para la función potencial-exponencial, es aconsejable el empleo de la derivación logarítmica, ya que facilitan bastante el cálculo.

4.3 - Diferenciación implícita:

Se dice que una función está definida explícitamente cuando se da de la forma y = f (x); esto es cuando se da y despejada en términos de x. En cambio, si en una ecuación, como por ejemplo, 2yx = cos3y, existe una función tal que y = f (x), se dice que y es una función que está definida implícitamente por la ecuación. Una ecuación en x e y puede definir a más de una función implícita.
v    En muchas ocasiones no se puede resolver explícitamente una función dada en forma implícita.
v    Es posible hallar la derivada de una función expresada implícitamente, sin necesidad de transformarla en su equivalente explícita.

aquí podrán ver un ejemplo de como hacerlo

https://www.youtube.com/watch?v=oneC1gsSQaM

4.2 - Derivadas de funciones exponenciales:

La derivada de la función exponencial ea igual a la misma función por el logaritmo neperiano de la base y por la derivada del exponente.

La derivada de la función exponencial de base e ea igual a la misma función por la derivada del exponente.

4.1 - Derivadas de funciones logarítmicas:

En el ámbito de las matemáticas, específicamente en el cálculo y el análisis complejo, la derivada logarítmica de una función f queda definida por la fórmula

donde f ′ es la derivada de f.

Cuando f es una función f(x) de una variable real x, y toma valores reales, estrictamente positivos, esta es entonces la fórmula para (log f)′, o sea, la derivada del logaritmo natural de f, como se deduce aplicando directamente la regla de la cadena.

tercer periodo

en este apartado veremos lo que son las derivadas y unas de sus reglas basicas para poder entenderlas y resolverlas

3.1 - Definición de la derivada:

En matemática, la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se torna cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado.

 

3.2 - Diferenciación de funciones por incrementos:

Diferenciación:
Incrementos y diferenciales.
Dada una función z = f(x, y), se llama incremento de la función, cuando x e y se incrementan ∆x e ∆y, a:
∆z = f (x + ∆x, y + ∆y) − f(x, y)

y se llama diferencial total a:
dz =
∂z
∂x dx +
∂z
∂y dy = fx(x, y) dx + fy(x, y) dy

3.3 - La derivada como razón de cambio.

El concepto de razón de cambio se refiere a la medida en la cual una variable se modifica con relación a otra. Se trata de la magnitud que compara dos variables a partir de sus unidades de cambio. En caso de que las variables no estén relacionadas, tendrán una razón de cambio igual a cero.

 

3.4 - Diferenciabilidad y continuidad:

El proceso de calcular la derivada de una función se denomina 'diferenciación ; esto es, la diferenciación es la operación mediante la cual se obtiene la función f'  a partir de la función f

Si una función tiene una derivada en x1 , se dice que la función es diferenciable en x1 . Una función es diferenciable en un intervalo abierto si es diferenciable en cada número del intervalo. Si una función es diferenciable en cada número de su dominio, entonces se dice que es una función diferenciable

Se concluye, por la definición 2.1.1 (ii)  que x=0 es la recta tangente a la gráfica de f en el origen

La función definida  por (x) =  tiene las siguiente propiedades

1.     f Es continua en 0

2.     f No es diferenciable en 0

3.    La grafica de f tiene una recta tangente vertical en el punto donde x=0

3.5 - Reglas básicas de derivación: 

Regla 1: Para una constante "a"
Si f(x)= a, su derivada es f '(x)= 0
Ejemplo: Si f(x)= 15 , su derivada es f '(x)= 0


Regla 2: Para la función identidad f(x)= x
Si f(x)= x, su derivada es f ' (x)= 1
Ejemplo: f(x)= x , su derivada es f '(x)= 1


Regla 3: Para una constante "a" por una variable x
Si f (x)=ax , su derivada es f '(x)= a
Ejemplo: si f (x)= 12x, su derivada es f '(x)= 12

Regla 4: Para una variable "x" elevada a una potencia "n"

Si f(x)= x , su derivada es f´(x)=nx
3 2
Ejemplo: f(x)= x, su derivada es f´(x)= 3x

Regla 5: Para una constante "a" por una variable "x" elevada a una potencia "n"
n n-1
Si f(x)= ax , su derivada es f´(x)= anx
2
Ejemplo: f(x)= 4x, su derivada es f´(x)= 8x

Regla 6: Para una suma de funcionesSi f(x)= u(x) + v(x), su derivada es f´(x)= u´(x) + v´(x)2Ejemplo: f(x)= 3x + 4x, su derivada es f´(x)= 6x+4

Regla 7: Regla del producto
Esta regla es útil cuando se tiene una función formada de la multiplicación de polinomios,
3 4Ejemplo: f(x)= (2x+3)(3x-5)2 4 3 3f´(x)=(6x )(3x-5) + (2x+3)(12x )
 Regla 8: Regla del cocienteEsta regla es útil cuando se tiene una función formada de la división de polinomios, comoSi "u" y "v" son los polinomios 2La función f(x)= u/v, Se deriva u´v - uv ´/v3 4Ejemplo: f(x)= 2x+3 / 3x-52 4 3 3 4 2f´(x)= (6x )(3x-5) - (2x+3)(12x ) / (3x-5)

Regla 9: Regla de la cadena
Esta regla útil cuando se tiene una función formada por un polinomio elevado auna potenciaSi "u" es el polinomion n-1La función: f (x) = u, Su derivada f´(x)= n(u) (u´)3 5Ejemplo: f(x)= (2x+3)3 4 2f´(x)= 5(2x+3) (6x )2 3 4f´(x)= 30x (2x+3)

3.6 - La regla de la cadena y de la potencia:

La regla de la cadena es una fórmula para calcular la derivada de la composición de dos o más funciones. Esto es, si f y g son dos funciones, entonces la regla de la cadena expresa la derivada de la función compuesta f ∘ g en términos de las derivadas de f y g. Por ejemplo , la regla de la cadena de f ∘ g (x) ≡ f [g (x)] es

o escrito en notación de Leibniz.

segundo periodo:

2.1 - Definición de límite.

En matemática, el concepto de límite es una noción topológica que formaliza la noción intuitiva de aproximación hacia un punto concreto de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor.

2.2 - Propiedades de los límites:

Propiedades de los límites

Los límites forman una parte fundamental del cálculo en las Matemáticas. De hecho, el primer punto en el concepto del cálculo está marcado por los límites. Los límites pueden ser entendidos fácilmente al observar sus propiedades.

Las Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.

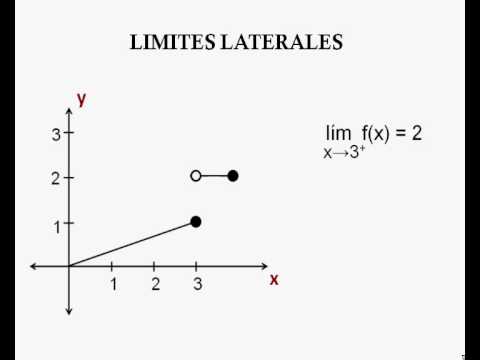
2.3 - Límites laterales:

Para que exista el límite de una función, deben existir los límites laterales y coincidir.

El significado de los signos en la notación para límites laterales se interpreta de la siguiente manera

• x ® a^- significa que x tiende a a tomando valores menores que a, es decir valores que se encuentran a su izquierda.

• x ® a⁺ significa que x tiende a a tomando valores mayores que a, es decir valores que se encuentran a su derecha.

2.4 - Límites al infinito:

cual es el resultado de 1/∞ ?

La razón más simple es que infinito no es un número, es una idea. Así que 1/∞ es un poco como decir 1/belleza o 1/alto.

A lo mejor podríamos decir que 1/∞ = 0 ... pero eso es un poco problemático, porque si dividimos 1 en infinitas partes y resulta que cada una es 0, ¿qué ha pasado con el 1?

De hecho 1/∞ es indefinido.

Así que en lugar de intentar calcular con infinito (porque no sacaremos ninguna respuesta razonable), vamos a probar con valores de x más y más grandes:

x	1/x
1	1.00000
2	0.50000
4	0.25000
10	0.10000
100	0.01000
1,000	0.00100
10,000	0.0001

Vemos que cuando x crece, 1/x tiende a 0

2.5 - Continuidad y discontinuidad:

Intuitivamente se puede decir que una función es continua cuando en su gráfica no aparecen saltos o cuando el trazo de la gráfica no tiene "huecos". En la figura 8.6., aparece la gráfica de tres funciones: dos de ellas no continuas (discontinuas) en el punto x = ade su dominio (fig. 8.6. (a) y 8.6. (b)) y la otra (fig. 8.6. (c)) continua en todo su dominio. 

no todas las funciones son continuas. Puede ocurrir que una función no sea continua en todo su dominio de definición. Si una función no es continua en un punto, se dice que la función tiene una discontinuidad en ese punto y que la función es discontinua. En este artículo se describe la clasificación de discontinuidades para el caso más simple de funciones de una sola variable real.

2.6 - Aplicaciones a las ciencias económico administrativas: interés compuesto continuamente, límite de la función costo promedio:

todo lo antes mencionado también se enfoca con la administración, porque con estos ejercicios  desarrollamos el pensamiento y eso nos facilitara ir mas mas allá de los números. 

funciones exponenciales y logarítmica:

función logarítmica

función exponencial

Aplicaciones en las ciencias económico administrativas: funciones de oferta y demanda; recta presupuestal, funciones de ingresos, costos y utilidades; funciones de apreciación y depreciación.

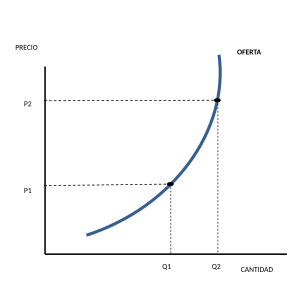grafica de oferta


gráfica de oferta

gráfica de demanda

primer periodo

1.1 - definición y notación de una función

el concepto general de función, aplicación o mapeo se refiere a una regla que asigna a cada elemento de un primer conjunto un único elemento de un segundo conjunto (correspondencia matemática). Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero):

...	−2 → +4,	−1 → +1,	0 → 0,
	+1 → +1,	+2 → +4,	+3 → +9,	...

Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. La definición general de función hace referencia a la dependencia entre los elementos de dos conjuntos dados.

1.2 - Dominio y Rango de una Función

El dominio de una función está dado por el conjunto de valores que puede tomar una función. Por ejemplo si f(x) = x;  esta variable x puede tomar cualquier valor, no tiene ninguna restricción, entonces su dominio esta compuesto por todos los números Reales.

El rango de una función, está determinado por todos los valores que pueden resultar al evaluar una función. Son los valores obtenidos para la variable dependiente (y). También se puede expresar como todos los valores de salida de la función.

Por ejemplo:

1.3 - Tipos de funciones:

Los tipos de funciones matemáticas

1.4 - Operaciones con Funciones:

ejemplos de operaciones con funciones

1.5 - Composiciones de funciones:

Si tenemos dos funciones: f(x) y g(x), de modo que el dominio de la 2ª esté incluido en el recorrido de la 1ª, se puede definir una nueva función que asocie a cada elemento del dominio de f(x) el valor de g[f(x)].

Veamos un ejemplo con las funciones f(x) = 2x y g(x) = 3x + 1.

1. (g o f) (x) = g [f(x)] = g (2x) = 3 (2x) +1 = 6x + 1
2.      (g o f) (1) = 6 · 1 + 1 = 7 

1.6 - Gráfica de una función:

las gráficas de las funciones solo se van mencionar las mas comunes y de las mas usadas en matemáticas.

1.7 - Función cuadrática y lineal:

función lineal

se mencionaran otro tipo de garficas muy comunes las cuales son:

función cuadrática